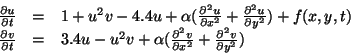
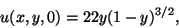

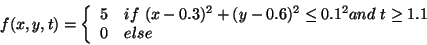
sources:
Examples of solution of stiff differential equations by explicit methods
Homepage
with initial condition: ![]()
and boundary conditions: ![]()
The function f is defined by : ![]()
sources:
solutions:
discussion:

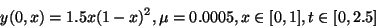 :
:
solutions:
discussion:
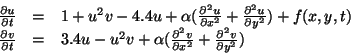
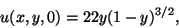

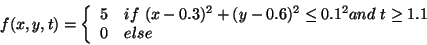
solutions:
discussion: