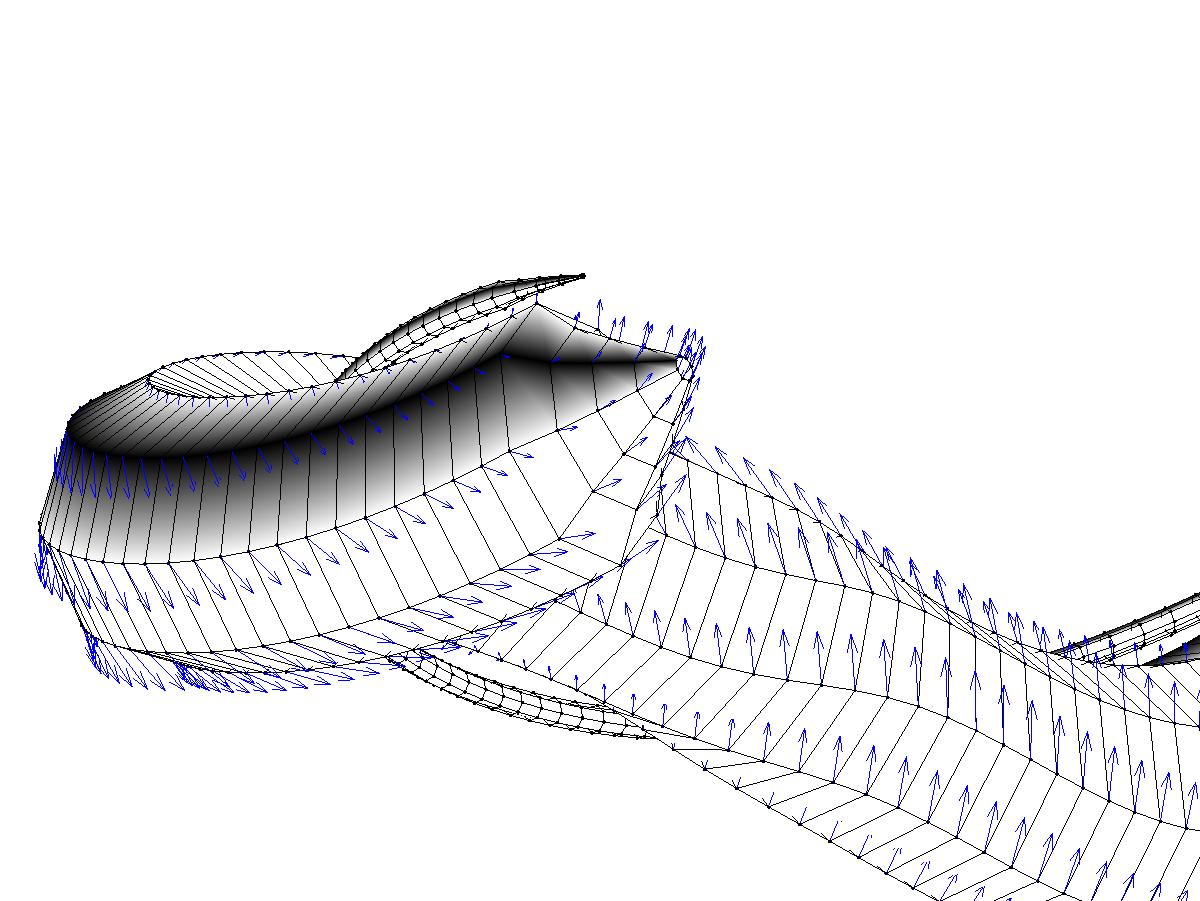
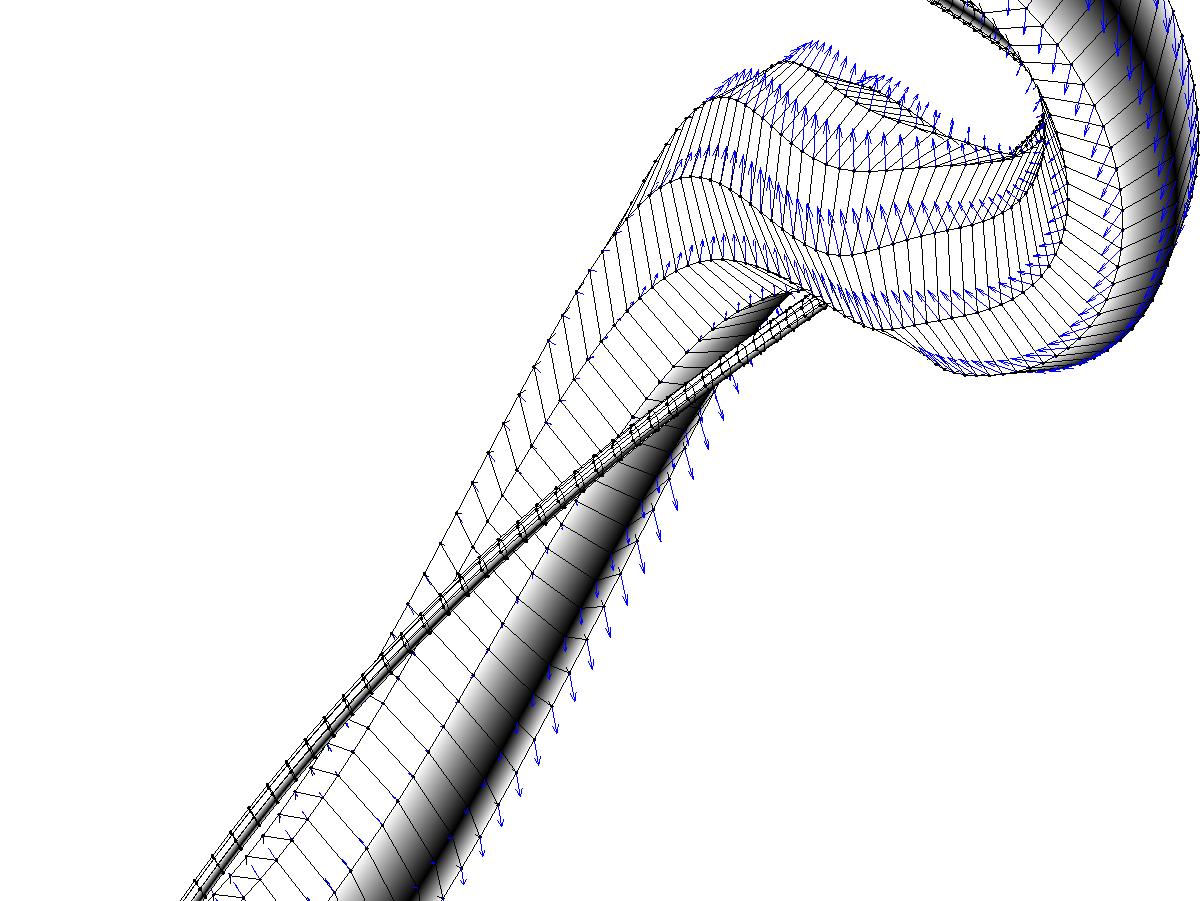
Mathematical modeling of motility of microorganisms.
Homepage 
Fluid dynamics usually described in terms of Navier-Stokes
equations. But microorganisms are so small that we can approximate non-linear
Navier-Stokes equations by linear Stokes equations. This simplification allows
to use reciprocal theorem (similar to the theorem used for Laplace equations in
order to derive solution in terms of Green functions) to derive solution of
Stokes equations in terms of integral equations (nice review of these methods
can be found in the book of Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized
Viscous Flow. Cambridge University Press.) In order to approximate
integral equations we've used method of regularized stokeslets, to describe boundary forces we've
used model of elastic spirochete's surface proposed by Lisa Fauci which is based on system of connected springs as well as
"motor" springs to simulate motors of real spirochete. For calculation of
resulting system of ordinary differential equations we've used high order explicit method for stiff differential equations. We've
calculated motion of spirochete as an elastic body as well as global swimming
characteristics (rotational and translational resistance matrixes and ratio of
translational and rotational velocities) of the solid body of helical shape:
R. Cortez, L. Fauci, A. Medovikov 2003. The method of regularized stokeslets in three dimensions: analysis, validation,
and application to helical swimming., Physics of Fluids 17, 031504
2005(has been selected for the March 1, Volume 9, Issue 5, 2005 of Virtual
Journal of Biological Physics Research).
You can click here to download movie with result of our simulations of swimming spirochete into your computer. Don't be afraid to download more than one movie of spirochete, you need to download at least million of spirochetes to make your computer sick. In order to see beautiful images of this creature click here.